Sudut berpelurus adalah dua sudut yang saling berpelurus (suplemen), dimana jumlah dua sudut tersebut membentuk sudut lurus yang berarti sudut tersebut berukuran 180°. Contoh :

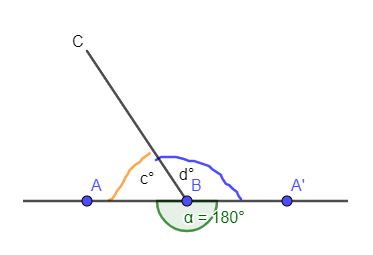
Gambar Sudut Berpelurus
Sehingga jika gambar di atas menunjukkan bahwa :
m∠ ABC = c° dan m∠ CBA’ = d°
maka
c°+ d° = 180°
c° = 90°- d°
d° = 90°- c°
Sudut berpenyiku adalah dua sudut yang saling berpenyiku (berkomplemen), dimana jumlah dua sudut tersebut membentuk sudut siku- siku yang berarti sudut tersebut berukuran 90°.
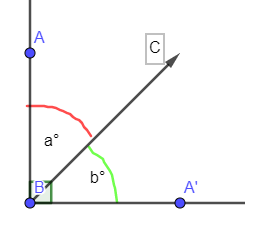
Gambar Sudut Berpenyiku
Sehingga jika gambar di atas menunjukkan bahwa :
m∠ ABC = a° dan m∠ CBA’ = b°
maka
a°+ b° = 90°
a° = 90°- b°
b° = 90°- a°
Pasangan sudut yang saling bertolak belakang terjadi jika terdapat dua garis berpotongan sehingga dua sudut yang letaknya saling membelakangi titik potongnya disebut sebagai dua sudut yang bertolak belakang. Besar dari dua sudut yang saling bertolak belakang sama besar.
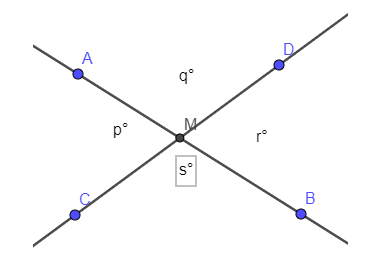
Gambar Sudut yang Saling Bertolak Belakang
Contoh pada gambar 27, pasangan ∠p° dan ∠r°dan pasangan ∠q° dan ∠s° merupakan sudut-sudut bertolak belakang. Selain itu, pada gambar tersebut, ∠q° dan ∠r°adalah pasangan sudut berpelurus dan ∠r° dan ∠s°a juga pasangan sudut berpelurus, sedemikian sehingga berlaku:
(1) q°+ r° = 180°, maka q° = 180° - r°
(2) s °+ r° = 180°, maka s ° = 180° - r°
Dari persamaan 1 dan 2 maka berlaku bahwa :
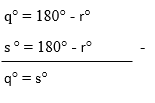
Dan dengan menggunakan cara yang sama, dapat diperoleh bahwa p° = r° juga pasangan yang bertolak belakang.

Gambar Hubungan Sudut- Sudut pada Dua Garis Sejajar
Suatu sudut yang mempunyai posisi yang sama serta besarnya pun sama. Pada gambar 28, sudut yang sehadap yaitu:
∠P1=∠Q1
∠P2=∠Q2
∠P3=∠Q3
∠P4=∠Q4
Suatu sudut yang terdapat dalam bagian dalam serta posisinya saling berseberangan. Dalam gambar 28 sudut dalam berseberangannya yaitu:
∠P4=∠Q2
∠P3=∠Q1
Suatu sudut yang terletak di bagian luar serta posisinya saling berseberangan. Dalam gambar 28 sudut luar berseberangannya yaitu:
∠P1=∠Q3
∠P2=∠Q4
Sudut yang terletak di bagian dalam serta posisinya terletak pada sisi yang sama. Jika dijumlahkan, sudut yang saling sepihak akan membentuk sudut 180°. Dalam gambar di atas sudut dalam sepihak yaitu:
∠P3+∠Q2 = 180°
∠P4+∠Q1 = 180°
Suatu sudut yang terletak di bagian luar serta posisinya terletak pada sisi yang sama. Jika dijumlahkan, sudut yang saling sepihak akan membentuk sudut 180°. Dalam gambar 28 sudut luar sepihak yaitu:
∠P1+∠Q4 = 180°
∠P2+∠Q3 = 180
Merupakan suatu sudut yang posisinya saling bertolak belakang, pada gambar 28 sudut yang bertolak belakang yaitu:
∠P1 = ∠P3
∠P2 = ∠P4
∠Q1= ∠Q3
∠Q2 = ∠Q4
Tentukan nilai x nya
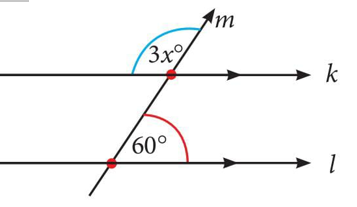
Penyelesaian :
Karena garis k//l, akibatnya besar sudut 3x dengan besar sudut 60° membetuk susut berpelurus
3x + 60°= 180°
3x = 180 °– 60°
3x = 120°
X = 40°
Jadi nilai x = 40°
Tentukan nilai x nya
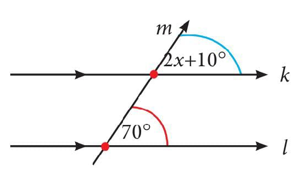
Penyelesaian :
Maka sudut (2x + 10) dengan sudut 70° merupakan sudut sehadap, sehingga kedua sudut tersebut besarnya sama, yakni sebagai berikut.
2x + 10 ° = 70°
2x = 70° – 10°
2x = 60°
X = 30°
Jadi, nilai x = 30°
Tentukan nilai x nya
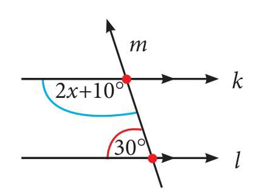
Penyelesaian :
Sudut (2x + 10°) dengan sudut 30° merupakan sudut dalam sepihak, sehingga kedua sudut membetuk sudut berpelurus, yakni sebagai berikut.
(2x + 10) + 30° = 180°
2x + 40° = 180°
2x = 180° – 40°
x = 70°
Jadi, nilai x = 70°
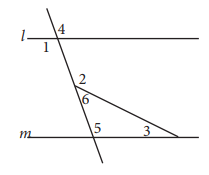
Besar sudut no 3 adalah 60° dan besar sudut nomor 5 adalah 85° maka besar sudut nomor 4 adalah...
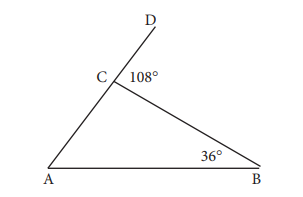
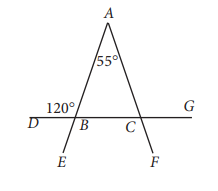
Besar sudut ∠CAB adalah...
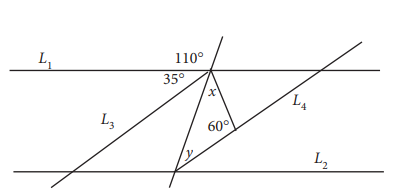
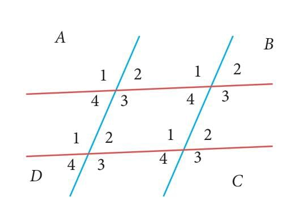
Diketahui garis L1 sejajar garis L2 dan garis L3 sejajar garis L4 . Besar sudut y – x adalah ….
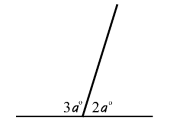
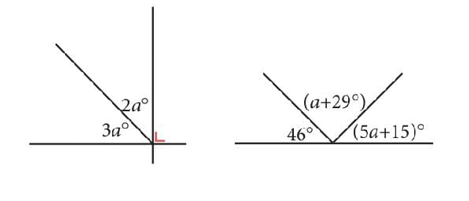
Nilai a adalah...
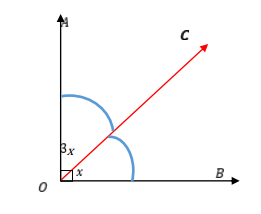
Nilai x adalah...
Hitunglah
Tentukanlah besar sudut: